Gravitation
Flashcards for topic Gravitation
Intermediate83 cardsGeneralFree
Loading...
Preview Cards
Card 1
Front
Back
Card 2
Front
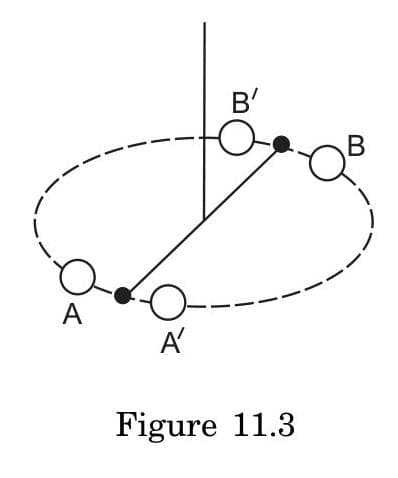
Back

Card 3
Front

Back

Card 4
Front

Back

Card 5
Front

Back

Card 6
Front

Back

Card 7
Front

Back

Card 8
Front
Back
Card 9
Front
Back
Card 10
Front
Back
Showing 10 of 83 cards. Add this deck to your collection to see all cards.